Das Märchen von der verteilten Terminierung

F. Mattern

Wohl wußte der König um den eigenwilligen aber steten Lebenswandel seiner Ratgeber, welche den ganzen Tag nichts taten, als zu essen und zu denken: War einer von ihnen bei Speis und Trank, so konnte alleine eine königliche Botschaft oder eine Nachricht eines anderen Weisen ihn zum Denken anregen - er griff meist sogleich zu Feder, Papier, Tinte und Siegel, um einigen übrigen Mitgliedern des so weit verteilten königlichen Konsiliums eine neue Weisheit zuzusenden. Hungrig vom Denken wandt er sich alsbald wieder der stets fürstlich gedeckten Tafel zu.

Als indes die Jahre vergingen und der König immer älter wurde, ohne daß er von den Weisen einen Rat erhalten hätte, seufzte er, schickte nach seinem geheimen Hofrat und sprach zu ihm: "Ich weiß wohl, wie schwierig ein gerechter Plan zur Aufteilung meines Erbes ist, und ich kenne die Regeln meines Konsiliums, wonach man mir erst kundtut, wenn die königliche Sache so erschöpfend beraten wurde, daß ein jeder der Weisen zufrieden ist und keine Botschaft mehr unterwegs ist. Alleine die königliche Post bereitet mir Sorge - ist etwa ein Schiff in den Stürmen der Meere gesunken oder hat sich ein Bote in der Weite des Reiches verirrt?"

"O königliche Hoheit", entgegnete der geheime Hofrat und sprach weiter: "Unermeßlich groß ist Euer Reich, und gar lange brauchen die Segler, um von einem Eiland zu einem anderen zu gelangen. Rein niemand vermag die Zeit vorher abzuschätzen, und es wird sogar berichtet, daß in der einen oder anderen Nacht ein Postboot ein anderes überholt. Aber die Segelkünste der Seefahrer, die hohe Schule der Schiffsbaumeister und die pflichtbewußte Ergebenheit Eurer Diener sorgen dafür, daß nicht eine einzige Botschaft verloren gehen kann. Lasset uns also Kundschafter aussenden, mein König, um jeden Ratgeber zu befragen, wieviele Botschaften er empfangen und versandt hat. So können wir leicht Gewißheit darüber erlangen, ob summa summarum so viele Nachrichten versandt wie empfangen wurden und das Konsilium des Königs Sache abschließend beraten hat."

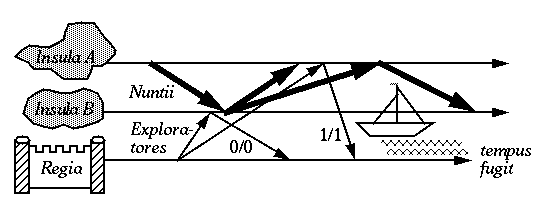
Der König war hoch erfreut über diese weisen Worte, schöpfte neue Zuversicht und beauftragte sogleich den Hofmathematicus, einen Plan auszuarbeiten. Dieser erschien alsbald mit einer großen Leinwand und sprach: "Majestät, auf diesem Szenario seht Ihr, daß des Hofrats Plan versagen kann - die zu den Eilanden A und B gesandten Kundschafter berichten, daß so viele Botschaften empfangen wie versandt wurden - summa summarum nur eine Botschaft. Nichtsdestotrotz sind noch Nachrichten unterwegs. Die Sache ist wohl so, daß die Kundschafter sehr klug vorgehen müssen, um sich nicht täuschen zu lassen und des Königs Zählung zu verfälschen, alldieweil wir primo die Uhr noch nicht erfinden konnten und somit auch keine einheitliche Reichszeit haben, secundo wir den Rundfunk noch nicht kennen und tertio die ehrwürdigen Sitten es verbieten, daß die Weisen an einem gemeinsamen Ort zusammenkommen." Der König war erstaunt über die gar wundersamen Worte und meinte: "Nun, das weiß ich wohl, denn ich bin der König. Was also rät Er mir ?" "Hoheit, mein Plan sieht vor, die Kundschafter erneut auszusenden, sobald der letzte bei Hofe eingetroffen ist. Wird alsodann das Ergebnis genau bestätigt und sind die Summen gleich, so ist keine Nachricht mehr unterwegs." "Vortrefflich", meinte der König, der nichts verstanden hatte. "Kümmere Er sich nur sogleich um die Instruktion der Kundschafter!"

Der Hofmathematicus tat wie befohlen, verbesserte seinen Plan noch verschiedentlich, und bald waren die Kundschafter, mit allen königlichen Vollmachten versehen, auf den besten Seglern des Reiches unterwegs zu den Weisen.

Als endlich der Schluß der Weisen bei Hofe eintraf, war der König so voll Glück, daß er den Hofmathematicus bald darauf zu seinem ersten Hofinformaticus ernannte. Und dieser forscht, wenn er nicht gestorben ist, noch heute in einem stillen Turm des königlichen Palastes... an einer noch besseren Lösung zum Problem der verteilten Terminierung!

Epilog

Papier war kostbar - so verzichtete der Hofinformaticus leider darauf, einen Korrektheitsbeweis seines Planes niederzuschreiben. Einer Randbemerkung seiner Schriften entnehmen wir, daß er später ein Verfahren ersann, bei dem nicht in jedem Fall die Inseln zwei- oder mehrfach von den Kundschaftern aufgesucht werden müssen. Des weitern gelang es ihm offenbar, die Zahl der notwendigen Kundschafterfahrten durch eine einfache Funktion der Zahl der Inseln und Botschaften zu beschränken. Leider reichte wieder einmal der Rand zur Darstellung der Methode nicht aus. Wer hilft mit bei der Rekonstruktion und Verifikation der Verfahren ?

Weiterführende Literatur

Beilken C, Mattern F, Reinfrank M (1985) Verteilte Terminierung - Ein wesentlicher Aspekt der Kontrolle in verteilten Systemen. Bericht SFB124-41/85, Fachbereich Informatik, Universität Kaiserslautern

Mattern F (1985) New Algorithms for Distributed Termination Detection in Asynchronous Message Passing Systems. Bericht SFB124-421/85, Fachbereich Informatik, Universität Kaiserslautern

Chandy K M, Misra J (1985) A paradigm for detecting quiescent properties in distributed computations. In: Apt K R (ed) Logics and models of concurrent systems. Springer-Verlag Berlin Heidelberg New York Tokyo, pp 325-341

Dijkstra E W, Scholten C S (1980) Termination detection for diffusing computations. Inf. Process. Lett. 11(1) : 1-4

Dijkstra E W, Feijen W H J, van Gasteren A J M (1983) Derivation of a termination detection algorithm for distributed computations. Inf. Process. Lett. 16(5) : 217-219

Francez N, Rodeh M (1982) Achieving distributed termination without freezing. IEEE Trans. Softw. Eng. SE-8(3) : 287-292